- CEMC Home
- About Us
- Contests
- Courseware
- CEMC Digital
- CEMC in Person
- Books
- Master of Mathematics
for Teachers - Educator Development
- Make a Difference
- Frequently Asked
Questions
Careers and Applications Flyer Solution 1
Problem 1
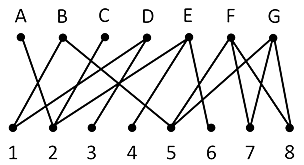
In the graph below, vertices A,B,C,D,E,F and G represent living kidney donors and vertices 1,2,3,4,5,6,7, and 8 represent patients in need of a kidney. The edges connecting pairs of vertices represent the compatible matches between donors and patients. What is the maximum number of patients that can be matched with a compatible donor?
|
 |
Note: A patient can only receive one kidney and a live donor only has one kidney to donate.
Problem 1 Solution
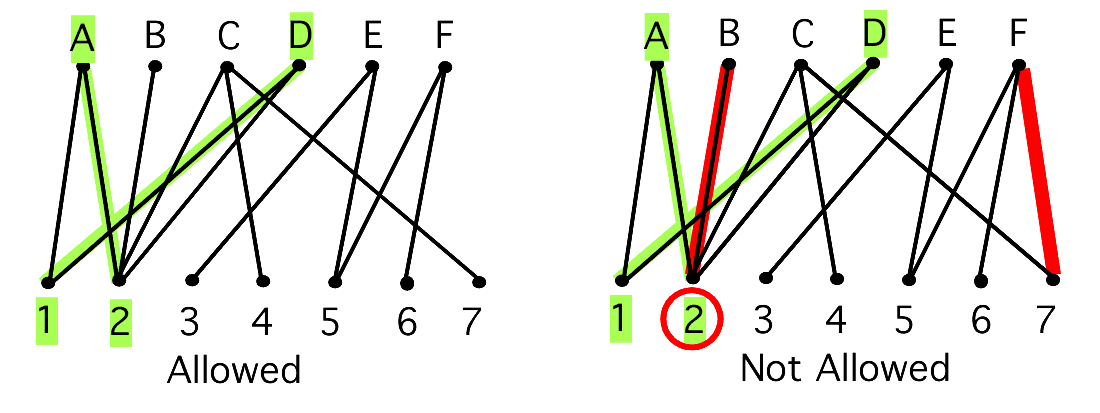
The problem asks us to use the given graph to match as many patients as possible with compatible donors. A patient and donor must be compatible and a donor can only receive one kidney and a donor only has one kidney to donate. |
 |
Using the graph, we can represent matching patients with compatible donors by colouring edges. We cannot colour two edges that connect to the same vertex and we cannot create a new edge. We must colour as many edges as possible in the graph.
After some careful colouring, we should come to the realization that we can colour at most 6 edges. We may have tried multiple colourings, but we are always stuck at 6.
Here is one way to colour 6 edges of the graph.
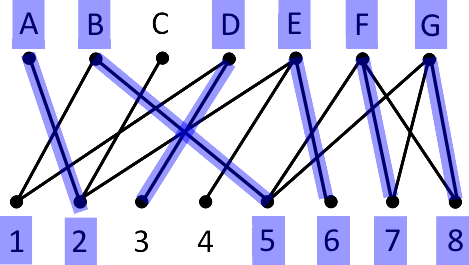
How can we be sure that there is no 7 or 8 edge colouring?
- Patients (verticies) 4 and 6 only connect to donor E, which means we must always leave 4 or 6 uncoloured.
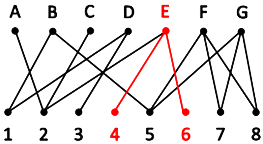
- Patients (verticies) 1, 3, 5, 7 and 8 connect only to donors B, D, F and G. That is 5 patients and 4 donors meaning one patient is always going to be left uncoloured.
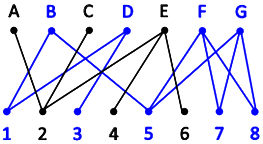
- In any colouring we now know that two patients (verticies) will always be uncoloured. Therefore the maximum edges that can be coloured is 6.
- Focusing on the donor vertices, we can make a similar argument showing that the maximum number of edges that can be coloured is 6.



 CEMC
CEMC