Skip to the content of the web site.

Behind the Scenes of Problem of the Week

By Jen Nelson

Problem of the Week (POTW) is a resource that is designed to provide students with an ongoing opportunity to work on solving mathematics problems. POTW is available at five levels: Problem A for students in Grades 3 and 4, Problem B for students in Grades 5 and 6, Problem C for students in Grades 7 and 8, Problem D for students in Grades 9 and 10, and Problem E for students in Grades 11 and 12. POTW launched in January 2011 at the C, D, and E levels, with level B following in September 2012 and level A following in September 2015. Since its launch, POTW has grown to have over 50 000 subscribers and a total of 1848 problems have been sent out.

This May will mark the completion of our 14th year of POTW. While we may be winding down the sending of problems for the school year, the planning for next year is just ramping up. Have you ever wondered what goes into creating this resource? I hope to give you a glimpse in this article!

The work on the A and B problems for the 2024/2025 year is well underway. The POTW A and POTW B resources are created by separate committees, each composed of a team of active teachers and chaired by a member of the CEMC. The POTW A and POTW B planning begins with the committees meeting over a weekend in November, where they work on a first draft of their 30 problems for the next school year. They meet again in February to revise and refine these problems. The chair of each committee then works through final edits of the problems and solutions over the months that follow, in hopes of having most of the year ready by September, as the planning for the next year will begin again in November!

At the C, D, and E levels, we're just beginning our work on the 2024/2025 year. At these levels, we have a team of three in the CEMC who are responsible for all problems and solutions. Two of these team members had previous careers as high school mathematics teachers, and their insight and experiences are invaluable to the POTW team. As a member of this team, I can speak more to the entire process of creation of this resource, from start to finish. At these levels, the planning for a year begins first by mapping out what “theme” or type of problem we would like to feature each week, for the entire 30 weeks, rather than searching for problems right away. By having a theme to each week, we're hoping that it is easy for a student or teacher to pick a problem at the right level for them, and to quickly find similar problems that are easier or harder.

Once that initial mapping is done, the work to create the problems begins! We think that a good POTW problem has something for everyone, and we're hoping to create a resource that can be used by teachers with their entire class. Thus, we look for problems that are easy entry, yet also give some challenge, perhaps have multiple solutions, and maybe even teach something along the way.

We often look to past CEMC contest problems and past POTW problems for inspiration, but other times our problems are entirely new. The level at which we put a problem (C, D, or E) is often decided by the mathematics concepts required, keeping in mind that C problems are geared toward students in Grades 7 and 8, D problems are geared toward students in Grades 9 and 10, and E problems are geared toward students in Grades 11 and 12. At other times the levels are determined by the mathematical maturity that we think is required to solve the problem.

As an example, I will consider the Week 30 C, D, and E problems from this year. Early on, when mapping out the plan for the 2023/2024 year, we decided we'd like to finish the year with something along the flavour of logic and computational thinking, with a “game” feel. For inspiration, we started with #18 on the 2016 Pascal Contest. I encourage you to try the problem before continuing to read the article.

Twelve chairs are evenly spaced around a circle. Starting at the chair labelled 3 and moving counterclockwise around the circle, there are two chairs with no labels, then a chair labelled 4, then a chair with no label, then a chair labelled x, then a chair with no label, then a chair labelled y, then four chairs with no labels, before arriving back at the chair labelled 3.

As it was, we thought that the insight to place the 1 and 2 first between the 3 and 4 was not enough of an easy entry into the problem. To make this an easier problem to get into, rather than giving the positions of the 3 and the 4, we decided to instead give the positions of the 1 and the 3. Our hope is that the resulting problem is much easier to get started in, but then requires the same logical thinking as in the original problem. After trying the original version on the Pascal contest, I encourage you to try our C problem and see if you agree.

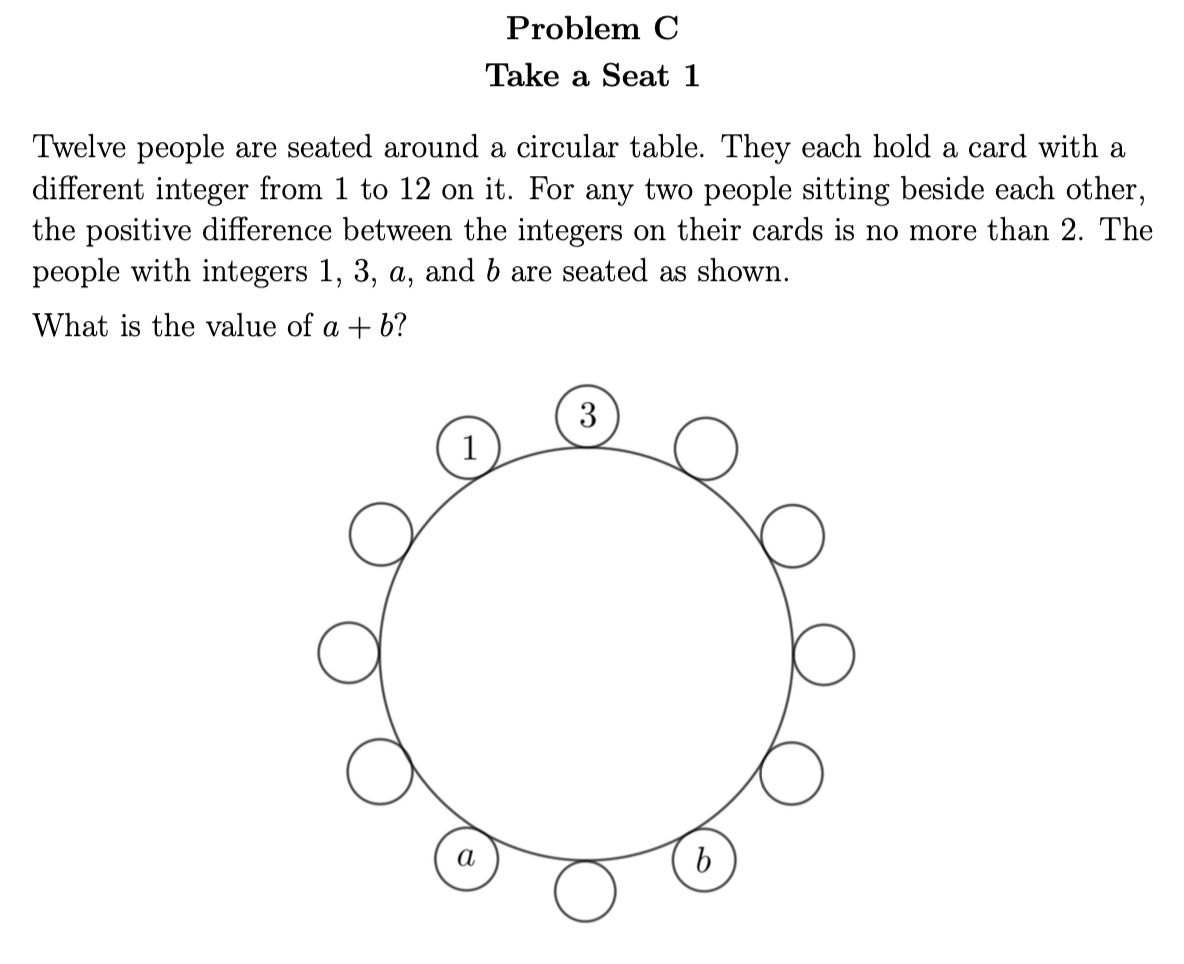
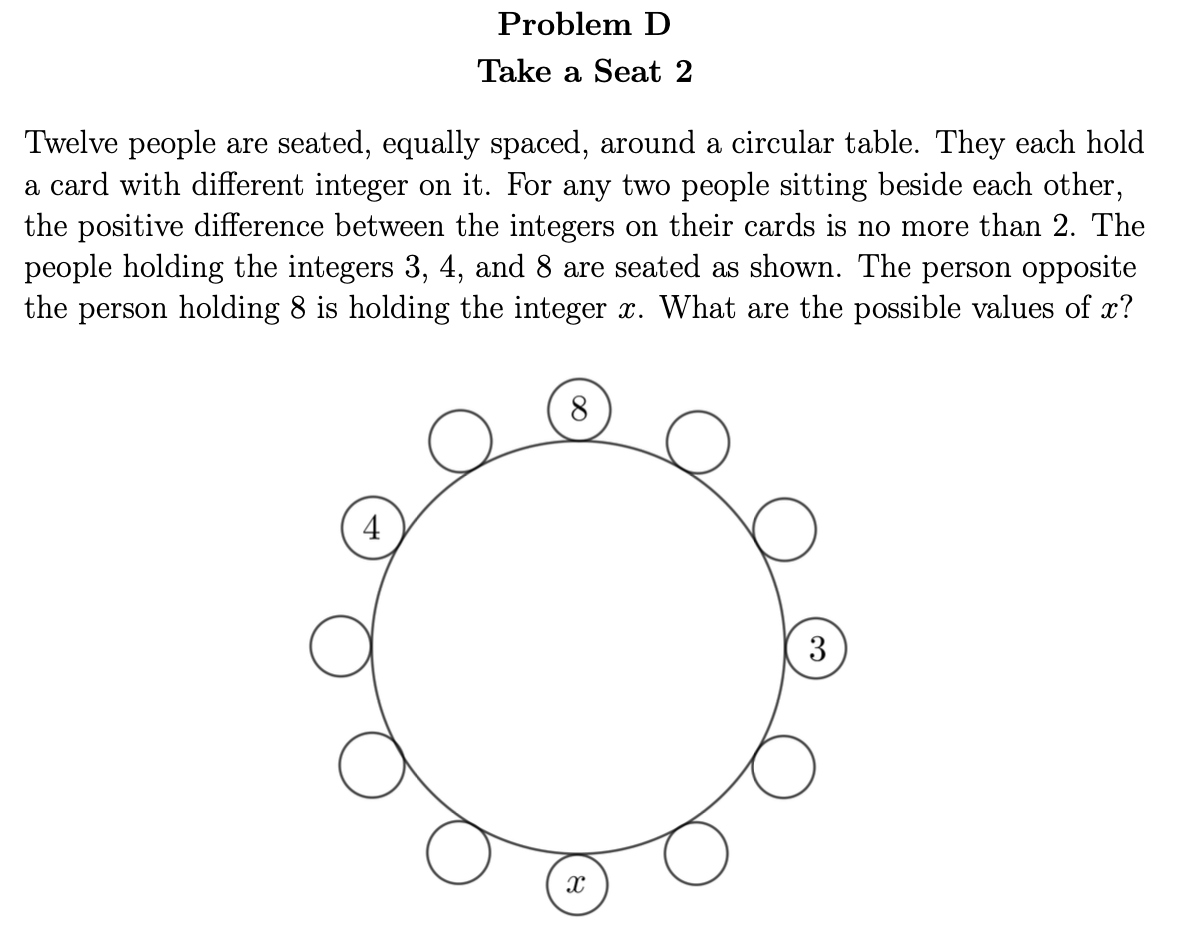
Twelve chairs are evenly spaced around a circle. Starting at the chair labelled 3 and moving counterclockwise around the circle, there is a chair labelled 1, then three chairs with no labels, then a chair labelled a, then a chair with no label, then a chair labelled b, then four chairs with no labels, before arriving back at the chair labelled 3.

After setting the C problem, our next task was to find D and E problems that were similar, but that required more mathematical maturity. When doing this for any problem, we usually start with trying to modify the problem we're trying to match. If we're unsuccessful in doing so, then we often move on to trying to find a different problem, but with the same theme.

For this problem, when we changed the parameters so that the cards have different integers on them, but not necessarily in the range from 1 to 12, and along with some careful consideration of what cards we gave to start, we were able to create a problem that was similar, but required the students to more carefully consider cases. Again, I encourage you to give this problem a try.

Twelve chairs are evenly spaced around a circle. Starting at the chair labelled 3 and moving counterclockwise around the circle, there is a chair labelled 1, then three chairs with no labels, then a chair labelled a, then a chair with no label, then a chair labelled b, then four chairs with no labels, before arriving back at the chair labelled 3.

Finally, our last task was to come up with an E problem to fit this theme. After spending time working through the case work in the D problem, we decided that it would be nice if we could create a problem where there ends up being more than one possible value of \(x\). That led to the following problem to complete the set:

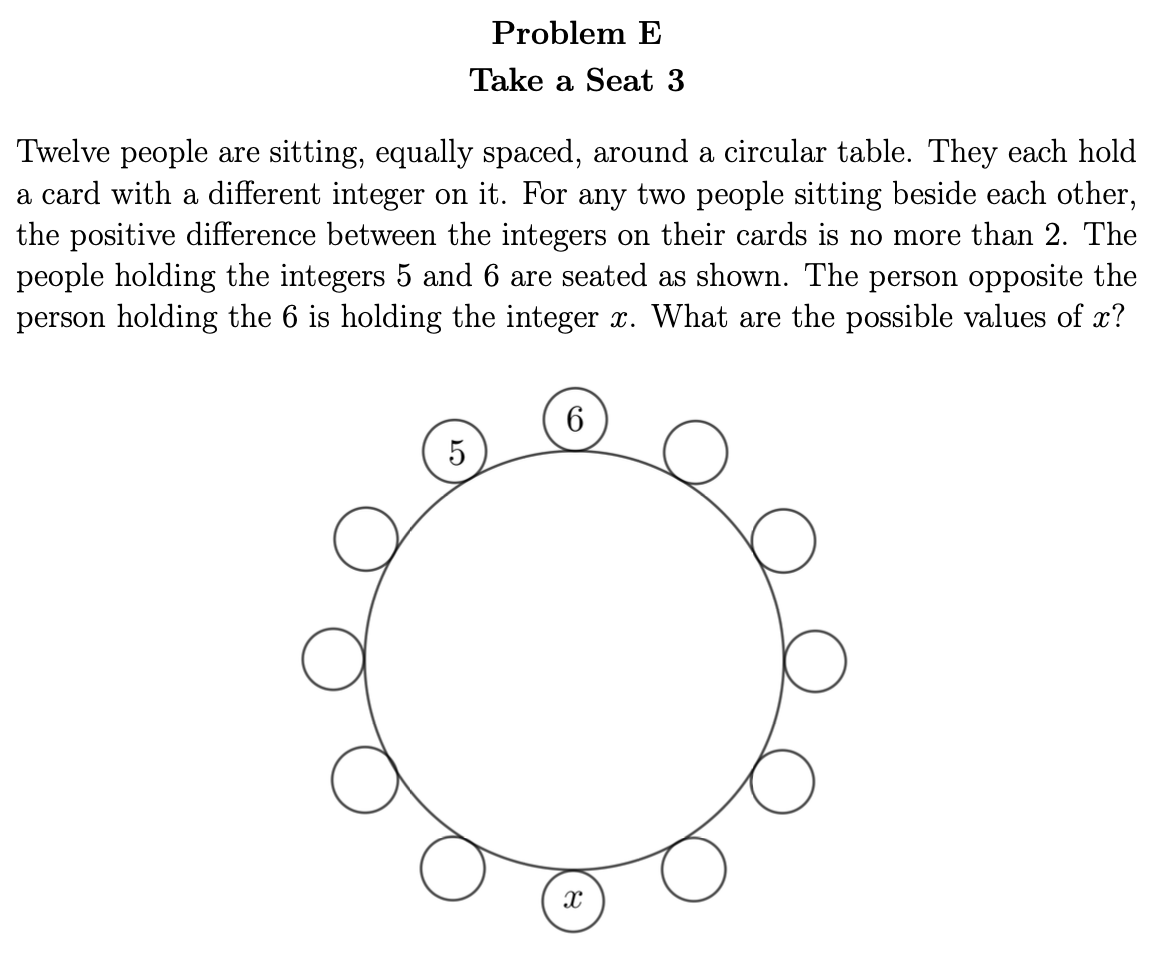
Twelve chairs are evenly spaced around a circle. The two chairs labelled 5 and 6 are side by side. The chair opposite 6 is labelled x.

In the end, we had a series of three problems that we were quite proud of. We think that the mathematical thinking required ramps up at each level, and we hope that working through earlier levels can help with gaining insight into how you might solve later levels.

I hope this article has given you a small glimpse into the teamwork, thinking, and processes that go into creating this popular resource. If you're interested in learning more about POTW or signing up to receive the weekly problems, you can do so here: https://cemc.uwaterloo.ca/resources/potw.php. If you already use this resource in your classroom, please consider sharing the POTW website with others.